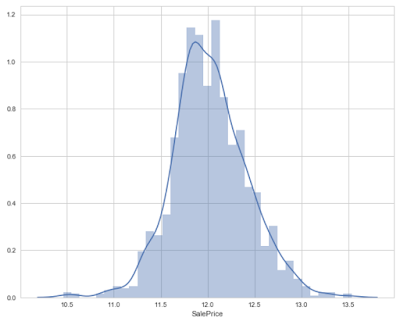
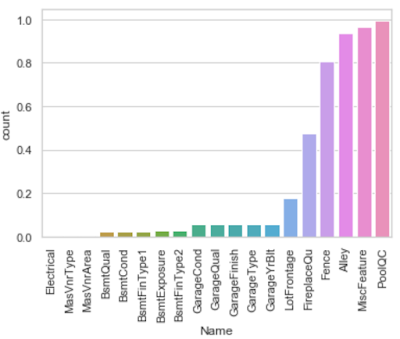
Lets try to find out the correlation among the variables in a dataset. Correlated variables don't provide any useful information to the model.We should remove correlated variables from the dataset for better accuracy and performance.
We will analyze the correlation among the variables through correlation heatmap using seaborn library in Python. corr method is used to find out the correlation. Then we will also find the correlation score of the variables with respect to target variable.
Consider Ames Housing dataset.
Step 1: Load the required libraries
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
Step 2: Load the dataset
dataset = pd.read_csv("C:/datasets/train.csv")
Step 3: Separate numeric and categorical variables
numeric_data = dataset.select_dtypes(include=[np.number])
categorical_data = dataset.select_dtypes(exclude=[np.number])
Step 4: Remove the Id column
del numeric_data['Id']
Step 5: Draw Correlation Heatmap
corr = numeric_data.corr()
plt.figure(figsize=(10, 10))
sns.heatmap(corr)
Notice the last row of this map. We can see the correlation of all the variables against SalePrice. As you can see, some variables seem to be strongly correlated with the target variable.
Step 6: Get Correlation Score
print (corr['SalePrice'].sort_values(ascending=False)[:10]) #top 10 correlations
print (corr['SalePrice'].sort_values(ascending=False)[-5:]) #least 5 correlations
Here we see that the OverallQual feature is 79% correlated with the target variable. Overallqual feature refers to the overall material and quality of the materials of the completed house. Well, this make sense as well. People usually consider these parameters for their dream house.
In addition, GrLivArea is 70% correlated with the target variable. GrLivArea refers to the living area (in sq ft.) above ground. The following variables show people also care about if the house has a garage, the area of that garage, the size of the basement area, etc.
We will analyze the correlation among the variables through correlation heatmap using seaborn library in Python. corr method is used to find out the correlation. Then we will also find the correlation score of the variables with respect to target variable.
Consider Ames Housing dataset.
Step 1: Load the required libraries
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
Step 2: Load the dataset
dataset = pd.read_csv("C:/datasets/train.csv")
Step 3: Separate numeric and categorical variables
numeric_data = dataset.select_dtypes(include=[np.number])
categorical_data = dataset.select_dtypes(exclude=[np.number])
Step 4: Remove the Id column
del numeric_data['Id']
Step 5: Draw Correlation Heatmap
corr = numeric_data.corr()
plt.figure(figsize=(10, 10))
sns.heatmap(corr)
Notice the last row of this map. We can see the correlation of all the variables against SalePrice. As you can see, some variables seem to be strongly correlated with the target variable.
Step 6: Get Correlation Score
print (corr['SalePrice'].sort_values(ascending=False)[:10]) #top 10 correlations
print (corr['SalePrice'].sort_values(ascending=False)[-5:]) #least 5 correlations
Here we see that the OverallQual feature is 79% correlated with the target variable. Overallqual feature refers to the overall material and quality of the materials of the completed house. Well, this make sense as well. People usually consider these parameters for their dream house.
In addition, GrLivArea is 70% correlated with the target variable. GrLivArea refers to the living area (in sq ft.) above ground. The following variables show people also care about if the house has a garage, the area of that garage, the size of the basement area, etc.